三角比って何?苦手意識を持つ前に知っておきたいこと
「三角比」と聞くと、高校数学の難しい分野というイメージを持つ方が多いのではないでしょうか?でも実は、三角比は私たちの身の回りで活用されている、とても実用的な数学なんです。
大人塾では、数学が苦手な方でも理解できるよう、三角比の基本をわかりやすく解説します。一度理解すれば「なるほど!」と納得できる分野ですよ。
三角比とは?日常生活での活用例
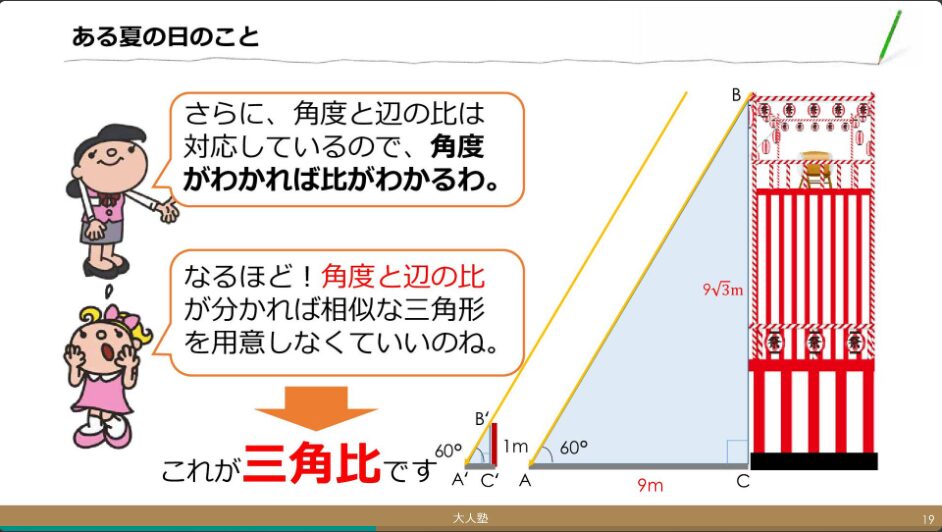
三角比とは、直角三角形の辺の長さの比を表したもの
身近な例:
- 建築・土木:屋根の傾斜角度の計算
- GPS・ナビ:位置や距離の測定
- ゲーム・CG:キャラクターの動きや3D描画
- 天体観測:星の位置計算
三角比の3つの基本:sin・cos・tan
sin(サイン)
sin A = 対辺 ÷ 斜辺 = b ÷ c
- 角Aの「向かい側の辺」と「斜辺」の比
- 0から1の間の値
cos(コサイン)
cos A = 隣辺 ÷ 斜辺 = a ÷ c
- 角Aの「隣の辺」と「斜辺」の比
- 0から1の間の値
tan(タンジェント)
tan A = 対辺 ÷ 隣辺 = b ÷ a
- 角Aの「向かい側の辺」と「隣の辺」の比
- sin ÷ cos でも計算できる
特別な角度の三角比
30°、45°、60°は覚えておこう
| 角度 | sin | cos | tan |
|---|---|---|---|
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | 1/√2 | 1/√2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
覚え方
45°の場合:正方形を半分に切った直角二等辺三角形で考える
- sin 45° = cos 45° = 1/√2
- tan 45° = 1(対辺と隣辺が等しいため)
まとめ
三角比は最初は難しく感じるかもしれませんが、基本的な考え方は「直角三角形の辺の比」というシンプルなものです。
大人塾では、このような「一見難しそうだけど、実は身近で実用的」な数学を、分かりやすく解説しています。大人になってからの学び直しでも、きっと「数学って面白い!」と感じていただけるはずです。