このレッスンでは真分数と仮分数と帯分数を学習します。
分数の概念が理解できている方が対象です。
分数にはタイプが3つがあります。タイプの見分け方や、変換の仕方などを学びましょう。
スライドはスマホで見る場合スライドしていただくこともできますし、キーボードの左右のボタンを利用していただくこともできます。
分数の3つの種類
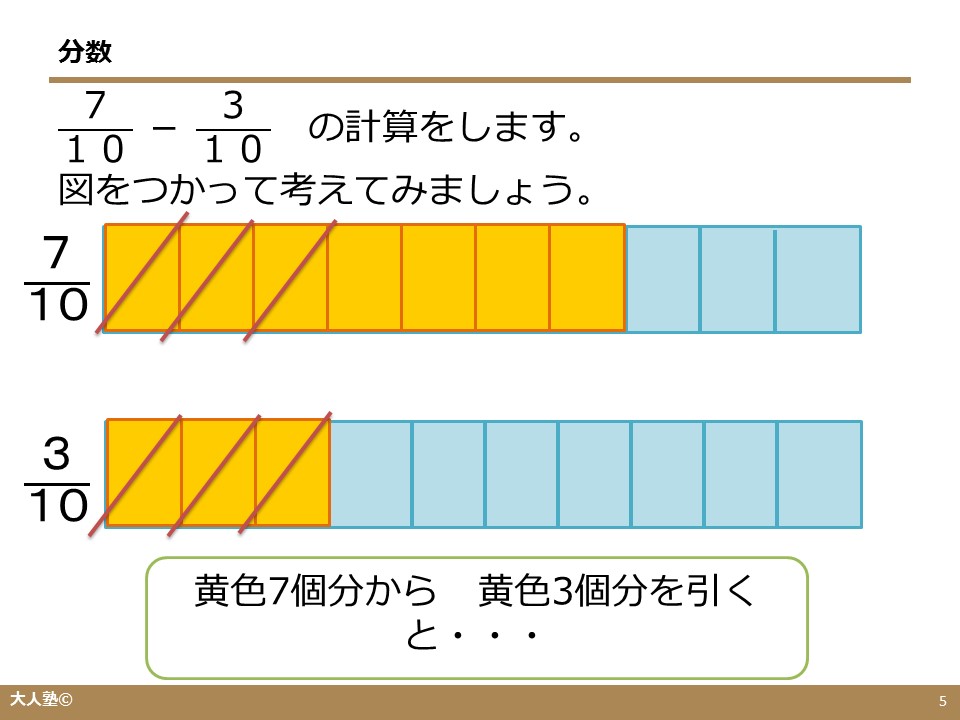
分数には実は「種類」があるんです。
名前は、真分数・仮分数・帯分数。
この名前は覚えなきゃいけない!っていうものではありません。
その代わり、ここで覚えていただきたいのは、
・どんな特徴?
・タイプの替え方
この2つに焦点を絞ってみていきましょう!
まず真分数。
特徴は「分子より分母が大きい」ことです。
簡単に言えば、下の数の方が大きい分数。
例えば、1/2などがあります。
そして小数に直すと「1より小さく」なります。
1/2も例外ではありません。
1÷2と1/2は同じなので、計算すれば0.5です。
なので1より小さくなります。
対して仮分数。
この特徴は「分子より分母が小さい」こと。
なので、小数に直すと「1より大きく」なる数です。
つまり、上の数の方が大きい分数ですね。
例えば、3/2のような分数です。
割り算に直して計算すると、
3÷2=1.5
となって1より大きくなりますよね。
じゃあ、帯分数はどうでしょう?
これは、「整数と分数の組み合わせ」で書かれます。
書き方や読み方は スライド8ページ目 を見てみましょう。
そして、整数がくっついているということは、
「1より大きい」分数です。
・・・あれ?
1より大きい分数って上でも出てきましたよね?
そう!
仮分数です!
実は、仮分数と帯分数は、書き方が違うだけ。
1より大きい分数であれば、
双方に「置き換え」ができてしまいます!
帯分数から仮分数に直す方法は スライド11ページ から。
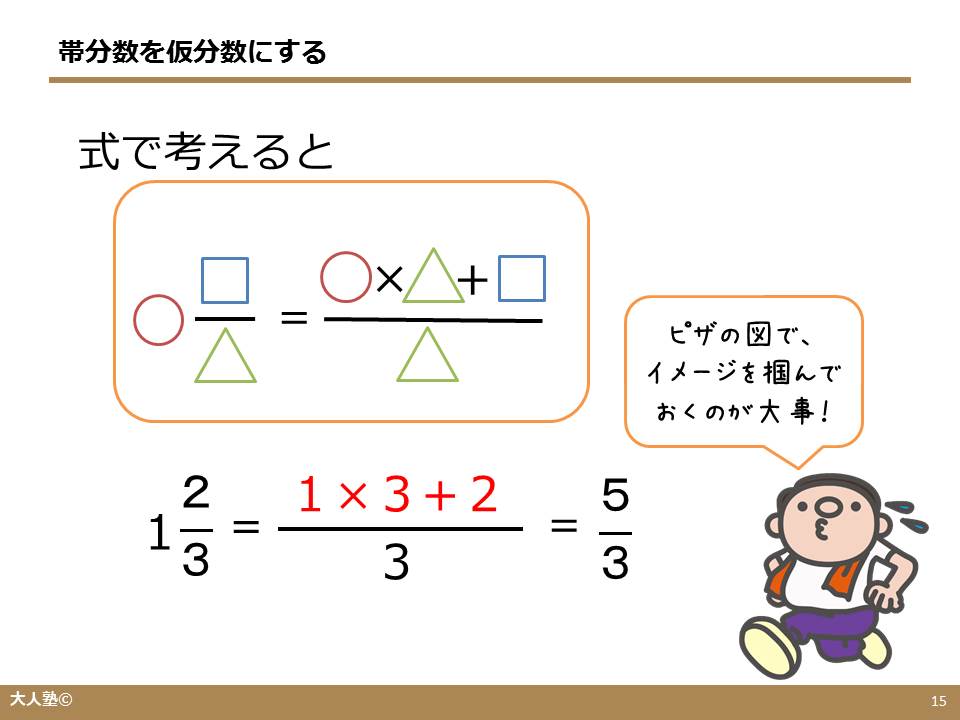
ピザを使った図を書いてみましょう。
帯分数は「整数と分数の組み合わせ」なので、
1と2/3なら、
ピザがまるまる1枚と、3等分されたピザ2枚分
ということになります。
まるまる1枚のピザを3等分すれば、
3等分のピザが5枚
ということになりますね。
なので、5/3と表すことができます。
逆に仮分数を帯分数に直すとき。
帯分数は、「整数と分数の組み合わせ」でした。
11/5を帯分数に直すのであれば、
11/5のなかに、1がいくつあるのかを調べます。
1を5/5と変形してあげれば、
5/5が2つと、残り1/5とできますね。
なので、2と1/5と変換できました。
この計算をよくよく見てみると
「余りのでる割り算」と同じ構造であることが分かります。
詳しい関係は、 スライド20ページを見てみましょう。
さて、いかがでしたでしょうか?
分数の種類といっても、何ということはありません。
特徴と変換の仕方だけマスターしてしまいましょう!